Trong đầu tư trái phiếu, để nhà đầu tư xác định tốt việc mua/bán trái phiếu và thu lại lợi nhuận thì việc định giá trái phiếu là vô cùng quan trọng. Thế nhưng, không phải nhà đầu tư nào cũng biết cách mà một trái phiếu được định giá trên thị trường như thế nào. Bài viết này sẽ giúp bạn hiểu rõ hơn về việc định giá trái phiếu để giao dịch tốt nhất. Theo dõi nhé!
Contents
Tìm hiểu tổng quan về định giá trái phiếu

Khái niệm
Định giá trái phiếu là việc xác định giá trị thực của một trái phiếu. Giá trị này bằng với giá trị hiện tại (hiện giá) của tất cả các dòng tiền nhận được trong tương lai được chiết khấu theo một lãi suất hợp lý.
Lãi suất chiết khấu khi định giá trái phiếu là lãi suất thị trường của một trái phiếu cụ thể. Đây cũng là lãi suất yêu cầu của nhà đầu tư. Lãi suất này thường được tính dựa trên lãi suất của trái phiếu chính phủ có cùng kỳ hạn và thời điểm đáo hạn, cộng thêm phần bù rủi ro.
Tìm hiểu thêm: LỢI SUẤT TRÁI PHIẾU
Quy trình định giá trái phiếu đến quyết định giao dịch

- Ước lượng dòng tiền sinh ra từ tài sản (thu nhập kỳ vọng).
- Ước lượng tỷ suất lợi nhuận NĐT yêu cầu (=lãi suất phi rủi ro +phần gia tăng do rủi ro).
- Lựa chọn mô hình định giá thích hợp để áp dụng. Tính hiện giá dòng tiền tệ thu nhập theo tỷ suất lợi nhuận vừa ước lượng.
- So sánh giá trị lý thuyết vừa định ra so với giá trị thị trường.
- Quyết định đầu tư (mua hay bán).
Công thức chung định giá trái phiếu

Công thức chung định giá trái phiếu
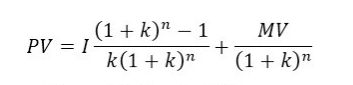
Trong đó:
- PV: giá trái phiếu cần xác định
- MV: mệnh giá trái phiếu
- i: lãi suất của trái phiếu
- I: cổ tức định kỳ
- k: lãi suất chiết khấu (lãi suất yêu cầu)
- n: số năm từ thời điểm đang xét đến đáo hạn
Giá trái phiếu bằng tổng giá trị hiện tại của các dòng tiền nhận được trong tương lai.
- Cổ tức định kỳ: I = i x MV (Vì cổ tức định kỳ là số tiền lãi mà người nắm giữ trái phiếu nhận được tại mỗi kỳ trả lãi)
Tham khảo: ĐẶT LỆNH MUA BÁN TRÁI PHIẾU IBOND ONLINE
Giải mã công thức
Xét dòng tiền của một trái phiếu như sau:
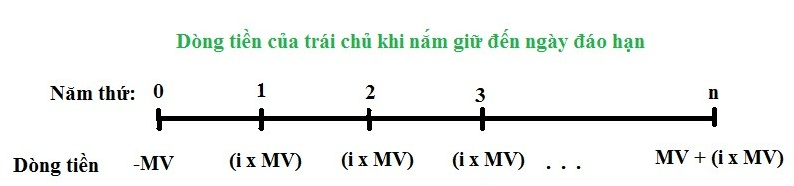
Theo định nghĩa, giá trái phiếu bằng với giá hiện tại của các dòng tiền trong tương lai. Vậy để xác định giá hiện tại của một dòng tiền cần làm như thế nào. Để tiếp cận khái niệm giá hiện tại (giá trị của thời điểm hiện tại) của dòng tiền bạn cần bắt đầu với một khái niệm đó là giá trị tương lai.
Giá trị tương lai sau n năm của một số tiền A ở thời điểm hiện tại là A (1 + r) n với r là lãi suất thị trường. Công thức này được hiểu rất đơn giản như sau: giả sử nhà đầu tư có $ 50 và thay vì cất giữ chúng, bạn gửi vào ngân hàng hoặc đầu tư vào một lĩnh vực nào đó. Với lãi suất cố định nhận được hàng năm là 10%.
- Sau thời gian một năm, số tiền nhà đầu tư nhận được sẽ bằng tiền gốc cộng với lãi = 50 + 50 x 0.1 = 50 (1+0.1) = 55$.
- Sau thời gian hai năm, số tiền nhà đầu tư nhận được sẽ là 55 + 55 x 10% = 50 (1+0.1) + 50 (1+0.1) x 0.1 = 50 (1+0.1) (1+0.1) = 50 (1+0.1)2$.
- Tương tự, sau n năm, số tiền người gửi nhận được sẽ là 50 (1+0.1)n$.
Theo đó, giá trị tương lai của 50$ sau một năm là 50(1+0.1)$. Sau hai năm sẽ là 50(1+0.1)2$ và sau n năm sẽ là 50(1+0.1)n$.
Cũng có thể nói rằng hiện giá (hay giá trị hiện tại) của khoản tiền 50(1+0.1)$ năm thứ nhất sẽ là 50$ = [50(1+0.1)]/(1+0.1). Hiện giá của khoảng tiền 50(1+0.1)2$ ở năm thứ 2 vẫn là 50$ = [50(1+0.1)2]/(1+0.1)2. Tương tự, hiện giá của 50(1+0.1)n$ ở năm thứ n sẽ cũng là 50$ = [50(1+0.1)n]/(1+0.1)n.
Từ đó:
- Giá trị tương lai sau n năm của một khoản tiền A ở thời điểm hiện tại là A(1+r)n.
- Hiện giá của A ở năm thứ n là A/(1+r)n hay A(1+r)-n.

Dòng tiền của trái phiếu:
- Hiện giá của dòng tiền năm thứ nhất là I/(1+k)
- Hiện giá của dòng tiền năm thứ hai là I/(1+k)2
- Hiện giá của dòng tiền năm thứ n là I/(1+k)n + MV/(1+k)n
Có thể suy ra:
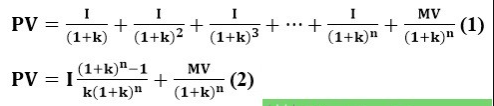
Đây là công thức chung về định giá trái phiếu.
Định giá trái phiếu

Định giá trái phiếu có kỳ hạn và lợi tức cố định theo từng kỳ
Công thức định giá của trái phiếu có kỳ hạn và lợi tức cố định theo từng kỳ cũng chính là được lấy từ công thức chung ở trên.
Ví dụ: Một trái phiếu có thời gian đáo hạn 10 năm, có mệnh giá 100,000 VND với lãi suất 10.5%. Định giá trái phiếu tại thời điểm phát hành với lãi suất yêu cầu là 12%.
Giá của trái phiếu sẽ là:
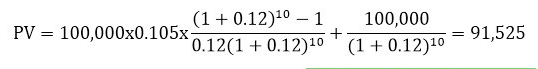
Định giá trái phiếu có kỳ hạn và không hưởng lợi tức định kỳ (Zero – coupon)

Zero – coupon là loại trái phiếu không được trả lợi tức định kỳ. Và người tham gia sẽ được mua nó với giá thấp hơn nhiều so với mệnh giá. Với loại trái phiếu này, lãi suất trái phiếu sẽ bằng 0 nên tất cả các khoản lợi tức I cũng sẽ bằng 0.
Cho nên, lúc này giá trái phiếu PV = MV/(1+k)n cũng chính là hiện giá của mệnh giá (MV) khi đáo hạn.
Ta xem xét ví dụ sau: Một trái phiếu zero-coupon có thời gian đáo hạn 10 năm, mệnh giá 100,000 VND. Định giá trái phiếu tại thời điểm phát hành với lãi suất chiết khấu 8%.
PV = 100,000/(1+0.08)10 = 46,319 VND.
Đọc thêm: TRÁI PHIẾU CHIẾT KHẤU LÀ GÌ?
Định giá trái phiếu có lãi suất thả nổi
Trái phiếu có lãi suất thả nổi chính là trái phiếu mà trái chủ sẽ nhận được các khoản lợi tức khác nhau, phụ thuộc vào lãi suất thị trường.
Lãi suất trái phiếu thả nổi = lãi suất thị trường + chênh lệch lãi suất cố định.
Đây là loại trái phiếu không được áp dụng theo công thức chung. Thế nhưng, để định giá nó chúng ta vẫn sẽ dựa vào khái niệm giá trị thực của trái phiếu.
Giá trái phiếu bằng với hiện giá của các dòng tiền nhận được trong tương lai.
Nếu nắm giữ từ lúc phát hành đến ngày đáo hạn, trái chủ của loại trái phiếu này sẽ nhận được các dòng tiền sau:
- Dòng tiền thứ nhất: lợi tức trả theo lãi suất thị trường và mệnh giá khi đáo hạn
- Dòng tiền thứ hai: các khoản tiền phụ trội từ khoản lãi suất chênh lệch cố định.
Dòng tiền thứ nhất cũng chính là dòng tiền thu được trong tương lai của trái phiếu. Nhưng lúc này sẽ theo lãi suất của thị trường thay vì theo một lãi suất cố định. Có nghĩa là hiện giá của dòng tiền thứ nhất cũng chính là giá trị thị trường của trái phiếu tại thời điểm phát hành. Tức là bằng với mệnh giá.
Đối với dòng tiền thứ hai, hiện giá được tính theo công thức bình thường vì các khoản tiền thu được là cố định.
Cho nên lúc này, công thức định giá của trái phiếu có lãi suất thả nổi là:
PV = Mệnh giá + Hiện giá của dòng tiền phụ trội
Gọi PT là phần phụ trội của trái phiếu, PT = MV x lãi suất chênh lệch cố định
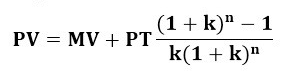
Định giá trái phiếu trả lãi theo định kỳ nửa năm
Khi trái phiếu là loại trả cổ tức theo định kỳ nửa năm một lần thì một số giá trị trong công thức định giá cũng sẽ thay đổi.
- Cổ tức nhận hằng kỳ là I/2
- Lãi suất yêu cầu của người tham gia hằng kỳ là k/2
- Tổng số kỳ là 2n.
Công thức định giá trái phiếu trả lãi theo định kỳ nửa năm là:
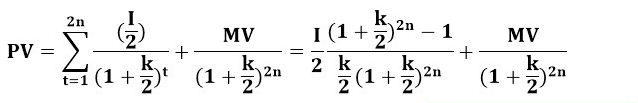
Mối quan hệ giữa giá trái phiếu và lãi suất chiết khấu

Để tìm hiểu về mối quan hệ giữa lãi suất chiết khấu và giá trái phiếu; hãy cùng theo dõi ví dụ sau:
Trái phiếu có thời gian đáo hạn là 10 năm, với mệnh giá 100,000 VND mức lãi suất 10.5% và trả lãi định kỳ hằng năm. Định giá trái phiếu tại thời điểm phát hành với lãi suất yêu cầu lần lượt là là 12%. 10.5% và 10%.
Lãi suất chiết khấu 12%, chúng ta suy ra giá trái phiếu từ công thức = 91,525 VND
Lãi suất chiết khấu 10.5%, suy ra giá trái phiếu = 100,000 VND
Lãi suất chiết khấu 10% thì suy ra giá trái phiếu = 103,072 VND
Như vậy bạn có thể xem kết quả trên, có thể thấy được mối quan hệ ngược chiều giữa lãi suất chiết khấu và giá của trái phiếu. Có nghĩa là khi lãi suất chiết khấu tăng thì giá trái phiếu giảm và ngược lại. Trường hợp khi lãi suất chiết khấu bằng lãi suất trái phiếu thì giá trái phiếu bằng với mệnh giá.
Bài viết đã chia sẻ cho bạn đọc về “ định giá trái phiếu là gì và cách định giá trái phiếu đơn giản và chi tiết nhất”. Hy vọng với những thông tin trên, các nhà đầu tư có thể nắm được cách định giá cơ bản trên thị trường; để từ đó có kế hoạch đầu tư phù hợp và chính xác hơn. Chúc các bạn có những quyết định giao dịch thật thành công!
Bài viết tham khảo:
- Trái phiếu Techcombank 2021
-
Khi nào lãi suất coupon bằng với lợi suất đáo hạn (YTM) của trái phiếu?
-
So sánh lợi suất đáo hạn (YTM) với lãi suất coupon của trái phiếu
